State Abbreviations Graph

In a recent chat that I participated in, we were discussing US two-letter state abbreviations that were one letter off of each other (e.g., NY and NJ).

After that discussion, I was curious about whether it would be possible to step from any state abbreviation to any other by changing one letter at a time, using only valid states along the way. My first step was to determine if there were any state abbreviations which didn’t share a first or last letter with any other states, so I wrote a simple Ruby script to test that.

state_codes = %w(AL AK AZ AR CA CO CT DE FL GA HI ID IL IN IA KS KY LA ME MD MA
  MI MN MS MO MT NE NV NH NJ NM NY NC ND OH OK OR PA RI SC SD TN TX UT VT VA WA
  WV WI WY)
state_codes.sort!
one_letter_changes = Hash.new()
state_codes.each do |sc|
  one_letter_changes[sc] = state_codes.select{
    |s| sc != s && (sc[0] == s[0] || sc[1] == s[1])
  }
  puts "#{sc}: #{one_letter_changes[sc].join(", ")}"
end

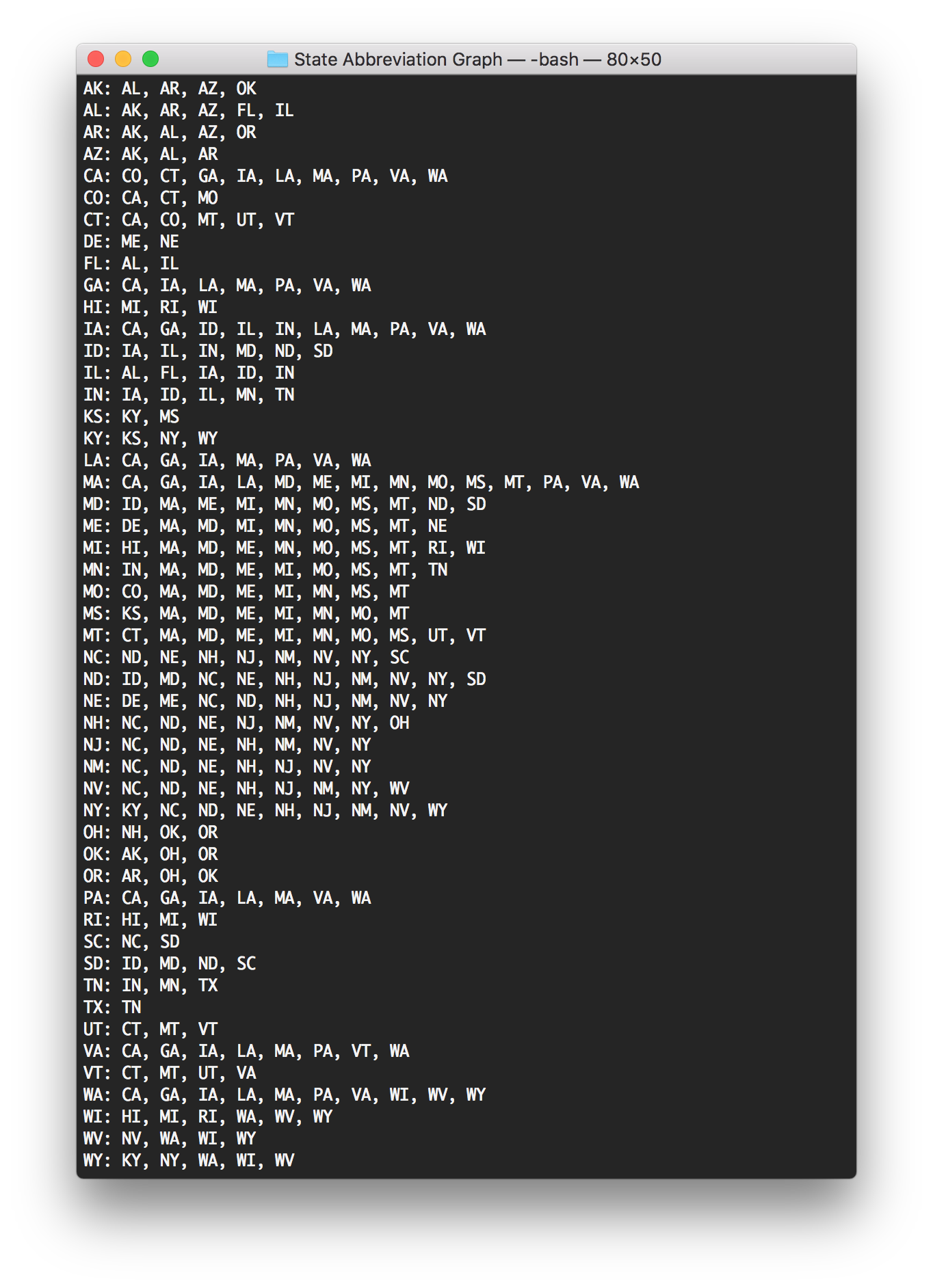
So every state had at least one other state it could go to. Texas (TX) had the fewest, with only Tennessee (TN); Massachusetts (MA) had the most, as quite a few state codes start with M or end with A.

Now I needed to find out if all the states would connect to each other, or if there would be several distinct “neighborhoods” of states. I decided to do this visually by creating a graph, using the output of my script to draw the connections:

Based on this graph, it is possible for any state abbreviation to change to any other state abbreviation!

I was also curious about the number of steps needed to go between any pair of state abbreviations, so I wrote a path distance algorithm based on Dijkstra’s algorithm (but with each path having equal weight) to find the shortest number of hops between any pair:

state_codes = %w(AL AK AZ AR CA CO CT DE FL GA HI ID IL IN IA KS KY LA ME MD MA
  MI MN MS MO MT NE NV NH NJ NM NY NC ND OH OK OR PA RI SC SD TN TX UT VT VA WA
  WV WI WY)
state_codes.sort!
one_letter_changes = Hash.new()
state_codes.each do |sc|
  one_letter_changes[sc] = state_codes.select{
    |s| sc != s && (sc[0] == s[0] || sc[1] == s[1])
  }
end

def path_distance(graph, source)
  vertexes = graph.keys
  return nil unless vertexes.include?(source)
  
  distance = Hash.new()
  previous_vertex = Hash.new()
  arbitrarily_large_distance = vertexes.length
  unvisited_vertices = Array.new

  vertexes.each do |v|
    distance[v] = arbitrarily_large_distance
    previous_vertex[v] = nil
    unvisited_vertices.push(v)
  end
  distance[source] = 0;

  while(unvisited_vertices.any?)
    min_distance_vertex = unvisited_vertices.min_by{|v| distance[v]}
    
    graph[min_distance_vertex].each do |neighbor|
      alt = distance[min_distance_vertex] + 1
      if alt < distance[neighbor]
        distance[neighbor] = alt
        previous_vertex[neighbor] = min_distance_vertex
      end
    end
    unvisited_vertices -= [min_distance_vertex]
  end

  return distance

end

state_codes.each do |code|
  values = path_distance(one_letter_changes, code).sort_by{
    |k,v| k}.reject{|k,v| k > code
  }.map{|d| d[1]}
  puts "#{code}  #{values.join("  ")}"
end
puts "   #{state_codes.join(" ")}"

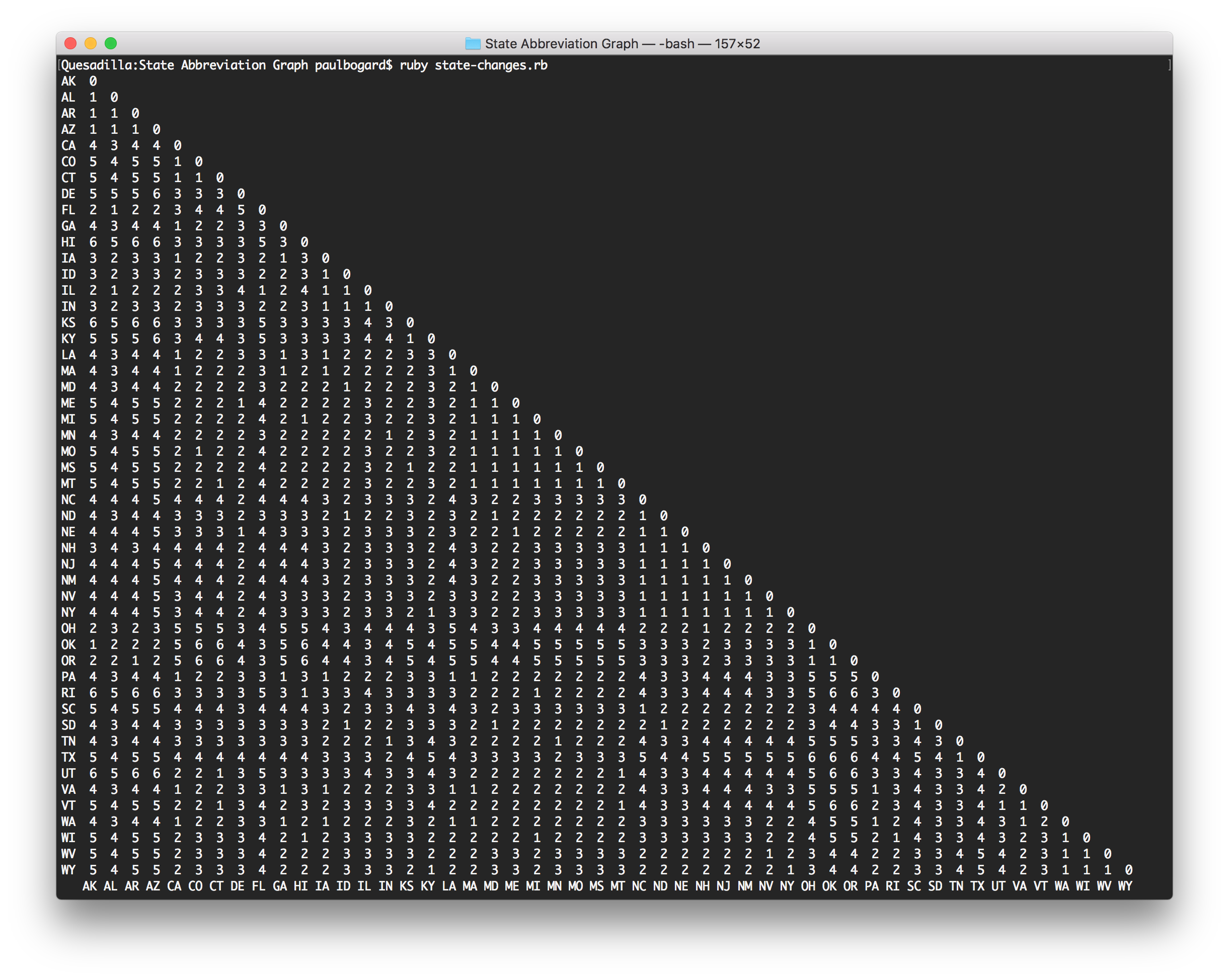
Based on the results, the highest number of hops is 6—so every state abbreviation can be changed into any other state abbreviation in at most six steps!